Non-Rocket Spacelaunch – Extraterrestrial Space Elevator Concepts

Earth is not the only planet that could have a space elevator. Variants of the basic space elevator design could also be built on other celestial bodies in the solar system. Most of those variants could fit into three categories: space elevators for rotating bodies (such as the Earth or Mars), space elevators for tidally locked moons or planets (such as Earth’s Moon or some of the Jovian moons) and space elevators for asteroids or other small bodies.

Martian space elevator

A Martian space elevator would follow the basic Earth space elevator concept, with the main difference that it would be much shorter than Earth’s. Mars’ surface gravity is 38% of Earth’s, while it rotates around its axis in about the same time as Earth. This puts the Martian areostationary orbit much closer to the surface, and hence the elevator would be much shorter. Current materials are already sufficiently strong to construct such an elevator.

However, building a Martian elevator would be a unique challenge because the Martian moon Phobos is in a low orbit, and intersects the equator regularly (twice every orbital period of 11 h 6 min). One solution would be to move the small moon into a higher orbit where it would pose no threat to the space elevator. Perhaps an easier solution would be to control the elevator’s oscillations so that it would move out of the moon’s path.

For an example of a Martian space elevator, read the science fiction trilogy by Kim Stanley Robinson starting with Red Mars.

Most other rotating celestial bodies could have a similarly designed space elevator, with the exception of slowly rotating bodies such as Venus, where a space elevator would be impractical.

Lunar space elevator

A lunar space elevator (also called a moonstalk) would be a much different design from the Earth’s counterpart. Since the Moon is tidally locked, the counterweight would have to be placed in a spot that remains stationary towards the Moon. Since there is no stationary orbit, only the L1 and L2 Lagrangian points would be suitable for such a purpose.

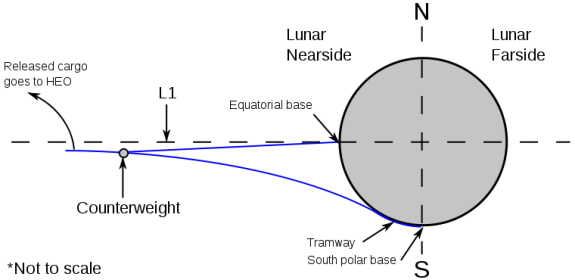
Lunar space elevator diagram. Image Credit: Star Technology and Research, Inc./Jerome Pearson

Both lunar-synchronous points are substantially farther up than the 36,000 km from Earth to geostationary orbit. Furthermore, the weight of the cable extending down to the Moon would have to be balanced by the cable extending further up, and the Moon’s slow rotation means the upper portion of the cable would have to be much longer than for an Earth-based system. To suspend a kilogram of cable or payload just above the surface of the Moon would require 1,000 kg of counterweight, 26,000 km beyond L1. Alternatively a smaller counterweight on a longer cable, such as 100 kg at a distance of 230,000 km (more than halfway to Earth) would have the same balancing effect.

For a space elevator anchored on the farside of the Moon, the counterweight would have to be located in the L2 Lagrangian point. Without the Earth’s gravity to attract it, an L2 cable’s lowest kilogram would require 1,000 kg of counterweight at a distance of 120,000 km from the Moon. Therefore, a space elevator on the nearside of the Moon using the L1 Lagrangian point would be much more cost-efficient and easier to build.

The anchor point of a space elevator is normally at the equator. However, because the Moon is tidally locked, the cable could be anchored nearly anywhere. Since the most efficient locations for lunar bases are at the poles on a peak of eternal light where they could take advantage of continuous solar power (and possibly exploit the small quantities of water and other volatiles that may be trapped in permanently shaded crater bottoms), a space elevator could be anchored near a lunar pole, though not directly at it. A tramway could be used to bring the cable the rest of the way to the pole, with the Moon’s low gravity allowing much taller support towers and wider spans between them than would be possible on Earth.

Because of the Moon’s lower gravity and lack of atmosphere, a lunar elevator would have less stringent requirements for the tensile strength of the material making up its cable than an Earth space elevator. This is why a lunar space elevator could be built using technologies and materials that are already available today. Also a lot of the safety issues of an Earth-based space elevator do not apply to the Moon.

One disadvantage of the lunar space elevator is that it may be too slow to carry human passengers. The rate at which cargo is transferred would normally take weeks to reach its destination. Humans would have to use other spacelaunch methods if they wanted to get there faster.

Asteroid space elevator

Rapidly spinning asteroids or moons could use cables to eject materials to convenient points (such as Earth orbits and Lagrangian points) or to eject materials to send the bulk of the mass of the object instead. In this case a miniature space elevator would be used as a slingshot.

Links to the other articles in this series

Space Elevator:

• Non-Rocket Spacelaunch – Space Elevator
• Non-Rocket Spacelaunch – Space Elevator Safety Issues
• Non-Rocket Spacelaunch – Space Elevators in Fiction

Tether Propulsion:

• Non-Rocket Spacelaunch – Tether propulsion
• Non-Rocket Spacelaunch – Tether satellite missions
• Non-Rocket Spacelaunch – Tether propulsion safety issues
• Non-Rocket Spacelaunch – Tether propulsion in fiction